机器学习数学推导
重参数化技巧 Reparameterization Trick 1
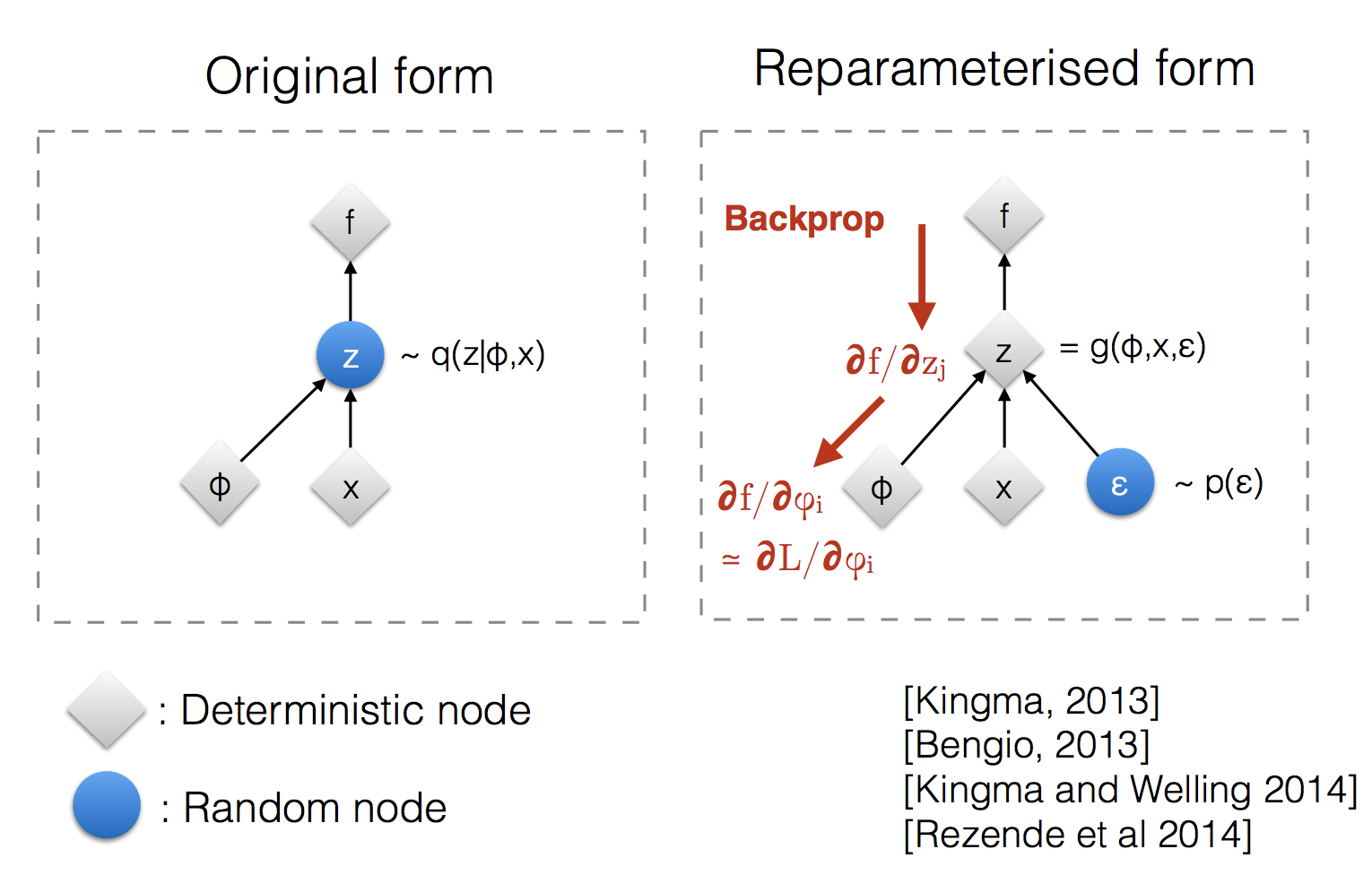
有时候loss函数中的某些项是从函数中 \(\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})\) 采样得到的,通过随机采样出来的数据是无法进行反向传播的。为了能够训练\(\phi\),我们将采样过程进行改变,求一个近似,使得 \(\mathbf{z}\) 变为确定性变量:\(\mathbf{z} = \mathcal{T}_\phi(\mathbf{x}, \boldsymbol{\epsilon})\),由 \(\phi\) 作为参数的 \(\mathcal{T}_\phi\) 将 \(\boldsymbol{\epsilon}\) 将 \(\boldsymbol{\epsilon}\) 进行转换。
举例来说,\(q_\phi(\mathbf{z}\vert\mathbf{x})\)通常是一个有对角线协方差的多变量高斯分布:
\[
\begin{aligned}
\mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\
\mathbf{z^{\prime}} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \\
\mathbf{z} &\approx \mathbf{z^{\prime}}
\end{aligned}
\]