三维坐标系介绍

三维直角坐标系是一个很常见的概念，任何的三维空间计算都需要用到三维直角坐标系。但是由于历史问题，在图形学中，没有制定统一标准，很多系统使用的坐标系标准都不太一样。在这篇文章中，我们进行一个介绍和梳理。

左手坐标系与右手坐标系

由于三维空间的复杂性，坐标轴的定义多种多样。这里先介绍一个概念：手性（Chirality）。

手性¹: 如果某物体与其镜像不同，则其被称为“手性的（英语：chiral）”，且其镜像是不能与原物体重合的，就如同左手和右手互为镜像而无法叠合。手性物体与其镜像被称为对映体（enantiomorph，希腊语意为“相对/相反形式”）；在有关分子概念的引用中也被称为对映异构体。可与其镜像叠合的物体被称为非手性的（achiral），有时也称为双向的（amphichiral）。

左手坐标系和右手坐标系无法通过旋转和位移重合。那么如何判断一个坐标系是左手坐标系还是右手坐标系呢？我们可以使用高中物理课时学到的右手螺旋定则，我们使用右（左）手大拇指朝向z轴正方向，如果x轴到y轴的方向符合其余手指的方向，则为右（左）手坐标系。如下图所示。

坐标系判断示意图

在右手坐标系中，能够直接使用数学运算和物理中的右手定则，而在左手坐标系中则需要对方向进行取反。建议使用右手坐标系，免得数学运算忘记取负出bug。

坐标系表示

然而即便同样是右手坐标系，每个系统中定义的轴的方向也不太一样。有的z轴方向向上，有的z轴方向向下，有的y轴向上，等等情况。

此时我们可以根据XYz轴的方向来标记坐标系。以COLMAP和OpenCV的坐标系为例，它们的坐标系中，x轴正方向向右R(ight)，y轴正方向向下D(own)，z轴正方向向前(Forward)，则该坐标系可以表示为RDF。

同理，Unity坐标系是左手坐标系，x轴正方向向右R(ight)，y轴正方向向上U(p)，z轴正方向向前F(orward)，则Untiy坐标系可以被表示为RUF。

至此，任意朝向的坐标系都能被这种方式表示出来。下图²展示了一些系统的坐标系表示。

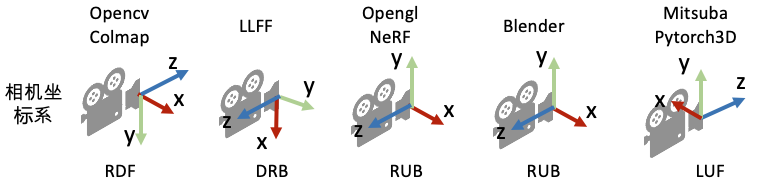
不同系统坐标系表示

常用系统坐标系表示

需要注意的是有些系统里面世界坐标系和相机坐标系不是一致的，比如Omniverse³（见下图）。

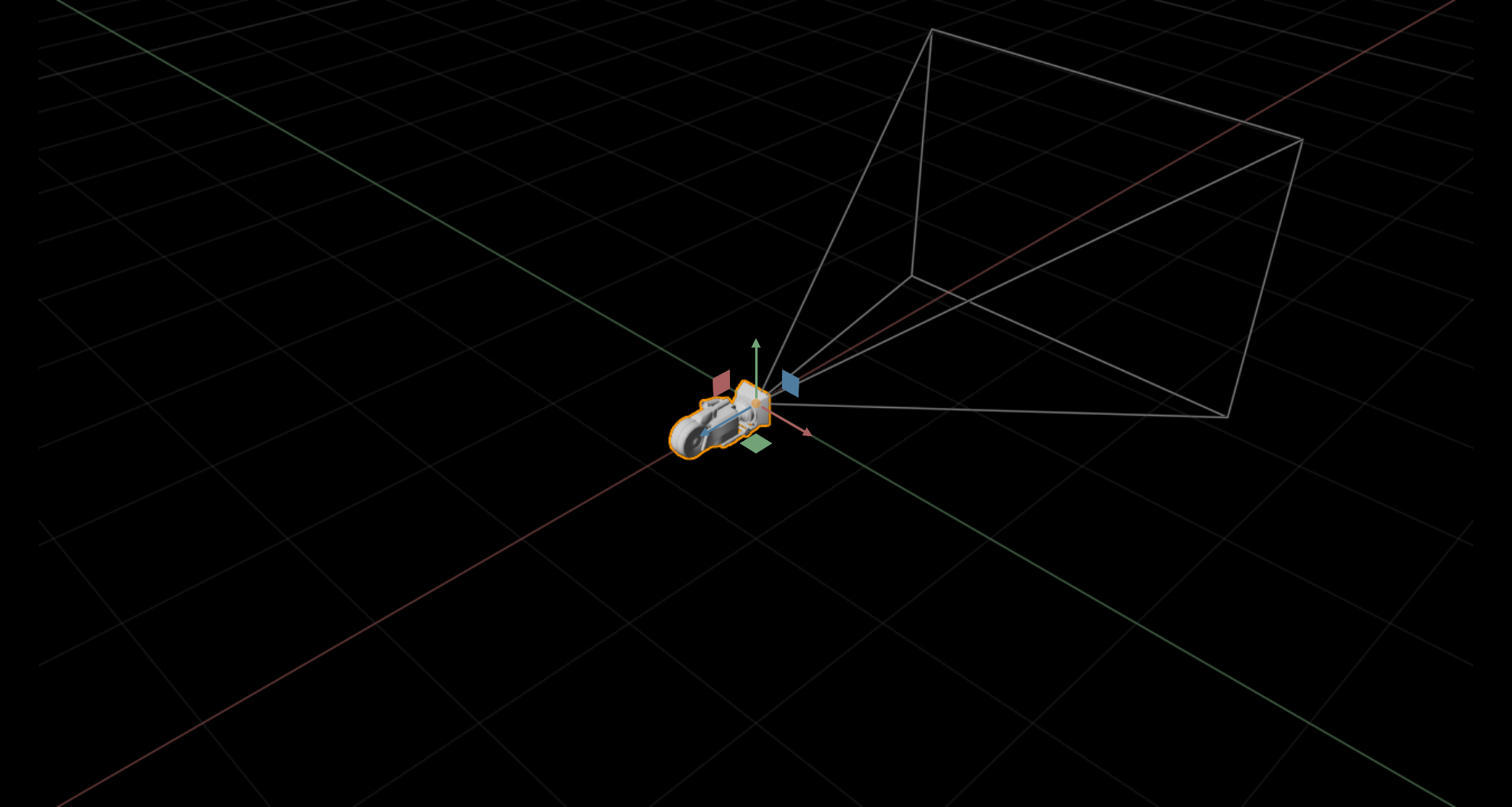
右手坐标系

系统	相机坐标系	世界坐标系
OpenCV	RDF	x
COLMAP	RDF	x
OpenGL	RUB	x
Blender	RUB	RFU
Omniverse	RUB	FLU
NeRF	RUB	x
Gaussian Splatting	RDF	x

左手坐标系

系统	相机坐标系	世界坐标系
Unity	RUF	RUF
Unreal	RBU	x

坐标系转换

既然我们发现已经有不同的坐标系表示了，那么我们应该如何把在自己的项目中统一起来呢，这个时候就需要用到坐标系转换了。

坐标系转换公式推导

我们先讲基础的二维坐标系变换。假设我们有两个坐标系\(xoy\)和\(uev\)和空间中的点\(\mathbf{p}\)，如下图³所示。

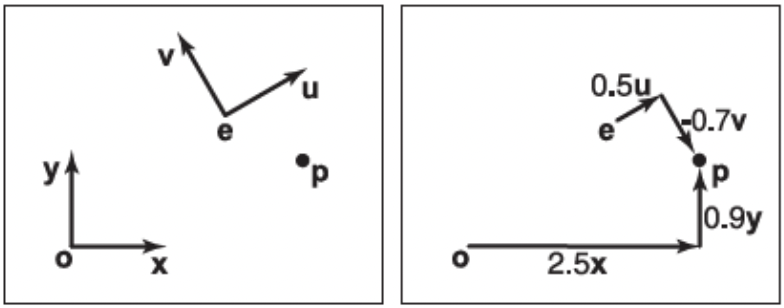
坐标转换示意图

在\(xoy\)坐标系内，\(\mathbf{p}\)可以被表示为：

\[ \mathbf{p}=(x_p,y_p) \equiv \mathbf{o} + x_p\mathbf{x}+y_p\mathbf{y} \]

同样的，\(\mathbf{p}\)在\(uev\)坐标系里可以被表示为：

\[ \mathbf{p}=(u_p,v_p) \equiv \mathbf{e} + u_p\mathbf{u}+v_p\mathbf{v} \]

如果，我们将\(\mathbf{e}\),\(\mathbf{u}\),\(\mathbf{v}\)用\(\mathbf{o}\),\(\mathbf{x}\),\(\mathbf{y}\)进行替换并用矩阵表示，则能够得到：

\[ \begin{equation} \left[\begin{array}{c} x_p \\ y_p \\ 1 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & x_e \\ 0 & 1 & y_e \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} x_u & x_v & 0 \\ y_u & y_v & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} u_p \\ v_p \\ 1 \end{array}\right]=\left[\begin{array}{ccc} x_u & x_v & x_e \\ y_u & y_v & y_e \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} u_p \\ v_p \\ 1 \end{array}\right] \end{equation} \]

通过矩阵的形式，我们可以将这个表达式看成是先旋转再平移。

简化以后得到另外一种表示：

\[ \mathbf{p}_{x y}=\left[\begin{array}{ccc} \mathbf{u} & \mathbf{v} & \mathbf{e} \\ 0 & 0 & 1 \end{array}\right] \mathbf{p}_{u v} \]

因为\(\mathbf{u}\),\(\mathbf{v}\)都是单位向量且正交，所以这个矩阵也就是由旋转和位移组成的转换矩阵。

同理，我们将\(\mathbf{o}\),\(\mathbf{x}\),\(\mathbf{y}\)用\(\mathbf{e}\),\(\mathbf{u}\),\(\mathbf{v}\)进行替换并用矩阵表示，能够得到：

\[ \begin{equation} \left[\begin{array}{c} u_p \\ v_p \\ 1 \end{array}\right]=\left[\begin{array}{ccc} x_u & y_u & 0 \\ x_v & y_v & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & -x_e \\ 0 & 1 & -y_e \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} x_p \\ y_p \\ 1 \end{array}\right] \end{equation} \]

这个形式也就是先平移再旋转，也就是公式(1)的逆变换。也就是：

\[ \mathbf{p}_{u v}=\left[\begin{array}{ccc} \mathbf{u} & \mathbf{v} & \mathbf{e} \\ 0 & 0 & 1 \end{array}\right]^{-1} \mathbf{p}_{x y} = \left[\begin{array}{ccc} \mathbf{x}_{uv} & \mathbf{y}_{uv} & \mathbf{o}_{uv} \\ 0 & 0 & 1 \end{array}\right]\mathbf{p}_{x y} \]

不同系统的坐标系转换

我们先介绍同一手性坐标系的转换，比如同为右手坐标系的转换。在这里我们以OpenCV坐标系到OpenGL为例，也就是从RDF坐标系到RUB坐标系。

在这里，我们使用RUB坐标系作为世界坐标系。那么，RDF坐标系中的x轴可以表示为\(\mathbf{x}^{RDF}_{RUB}=(1,0,0)^T\)，y轴可以表示为\(\mathbf{y}^{RDF}_{RUB}=(0,-1,0)^T\), z轴可以表示为\(\mathbf{z}^{RDF}_{RUB}=(0,0,-1)^T\)。

那么，我们很快就能构建出转换矩阵：

\[ \begin{aligned} \mathbf{p}_{RUB} &= \left[\begin{array}{cccc} \mathbf{x}^\mathrm{RDF}_\mathrm{RUB}& \mathbf{y}^\mathrm{RDF}_\mathrm{RUB}& \mathbf{z}^\mathrm{RDF}_\mathrm{RUB} & \mathbf{0} \\ 0 & 0 & 0 &1 \end{array}\right]\mathbf{p}_\mathrm{RDF} \\ &=\left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 &-1 & 0 & 0 \\ 0 & 0 &-1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\mathbf{p}_\mathrm{RDF} \end{aligned} \]

从这个矩阵也很好理解，将y轴取负，将z轴取负，则RDF坐标系就变成了RUB坐标系了。需要注意的是同手性坐标系转换矩阵的前三行前三列是旋转矩阵，可以用转置来求逆。而异手性的坐标系转换矩阵的前三行前三列不是旋转矩阵，不可以用转置来求逆。也就是说异手性的坐标系转换矩阵不是李群。

相机内外参

Misc

矩阵存储格式：

OpenCV row-major
Eigne column-major
CUDA column-major
glm column-major

Hugin一个可以转换各种投影的工具。

身处相机内外参之间（EG3D/NeRF/3D Gaussian Splatting）

家用微分几何 (第一话) 流形

【梦幻联动】家用微分几何与代数：李群

场论家用几何与代数（第一话）：李代数的崛起

关于你转生成为物理学家这档事

群论 (Group Theory) 终极速成 / 物理系零基础火箭级 notes

物理中涉及的数据处理方法

群论 (Group Theory) 终极速成 / 李群 (Lie group) 的定义与常见李群